前言
最近大伙儿们对R1的复现热情可谓是空前高涨,我也趁此机会,用家里的单卡3090,使用openr1+lora,尝试复现一把openr1-zero。
我的试验记录:
R1复现
https://docs.qq.com/aio/DZXBORFFUWEFPYnFG%3Fp%3DHVXAR5q2ACs0YdfYfsKPGT
实验效果
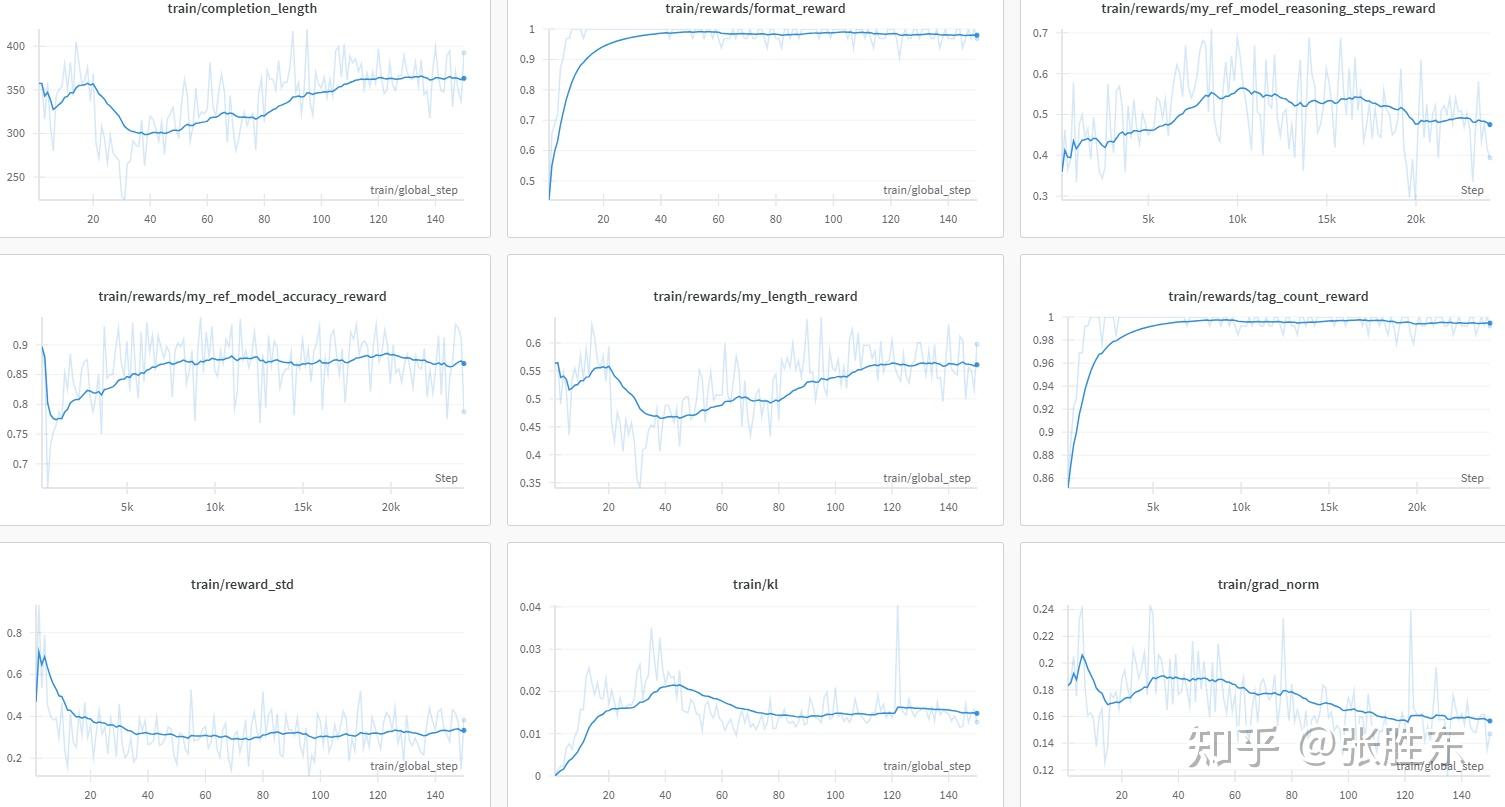
Qwen7B-Instruct模型+中文通用数据
1
2
3
4
5
6
7
8
9
10
| <|im_start|>system
You are a helpful AI Assistant that provides well-reasoned and detailed responses. You first think about the reasoning process as an internal monologue and then provide the user with the answer. Respond in the following format: <think>
...
</think>
<answer>
...
</answer><|im_end|>
<|im_start|>user
病毒的外壳和包膜结构如何影响它们不同的传播策略?<|im_end|>
<|im_start|>assistant
|
1
2
3
4
5
6
7
8
9
10
11
| <think>
首先,我们需要了解病毒外壳(衣壳)和包膜的基本结构。病毒的外壳通常由蛋白质组成,这些蛋白质围成一个壳体,保护病毒的遗传物质。而包膜则是由脂质双层组成,病毒通过感染宿主细胞后获取这些包膜。这些结构对病毒的传播具有不同的影响。
1. 衣壳:衣壳的作用是保护病毒的遗传物质不被环境中的酶降解,同时帮助病毒识别和附着到宿主细胞的受体。不同病毒的衣壳结构各异,这种差异可以影响病毒识别特定宿主细胞的能力,从而影响其传播方式。
2. 包膜:包膜的脂质双层来源于宿主细胞,它富含蛋白质和糖类,这些成分可以与宿主细胞上的受体结合,从而实现病毒的细胞融合。不同包膜蛋白的存在可以影响病毒的宿主范围和细胞侵入机制,从而影响其传播特性。
基于以上分析,我们可以得出结论:病毒的外壳和包膜在结构上的差异会导致其有不同的传播策略,例如通过特定的受体识别、细胞侵入机制等。这些特性决定了病毒在不同宿主细胞之间的传播效率和范围。
</think>
<answer>
病毒的外壳(衣壳)和包膜在结构上的差异会影响它们的传播策略。衣壳主要保护病毒遗传物质并帮助其识别宿主细胞,而包膜则有助于细胞融合和侵入。不同的结构特征使得病毒能够利用不同的宿主受体进行识别,利用不同的细胞侵入机制,从而影响其在宿主间的传播效率和范围。
</answer>
|
https://wandb.ai/bz-zhangshengdong/OpenR1/runs/ce7y7rgq%3Fnw%3Dnwuserzhangshengdong
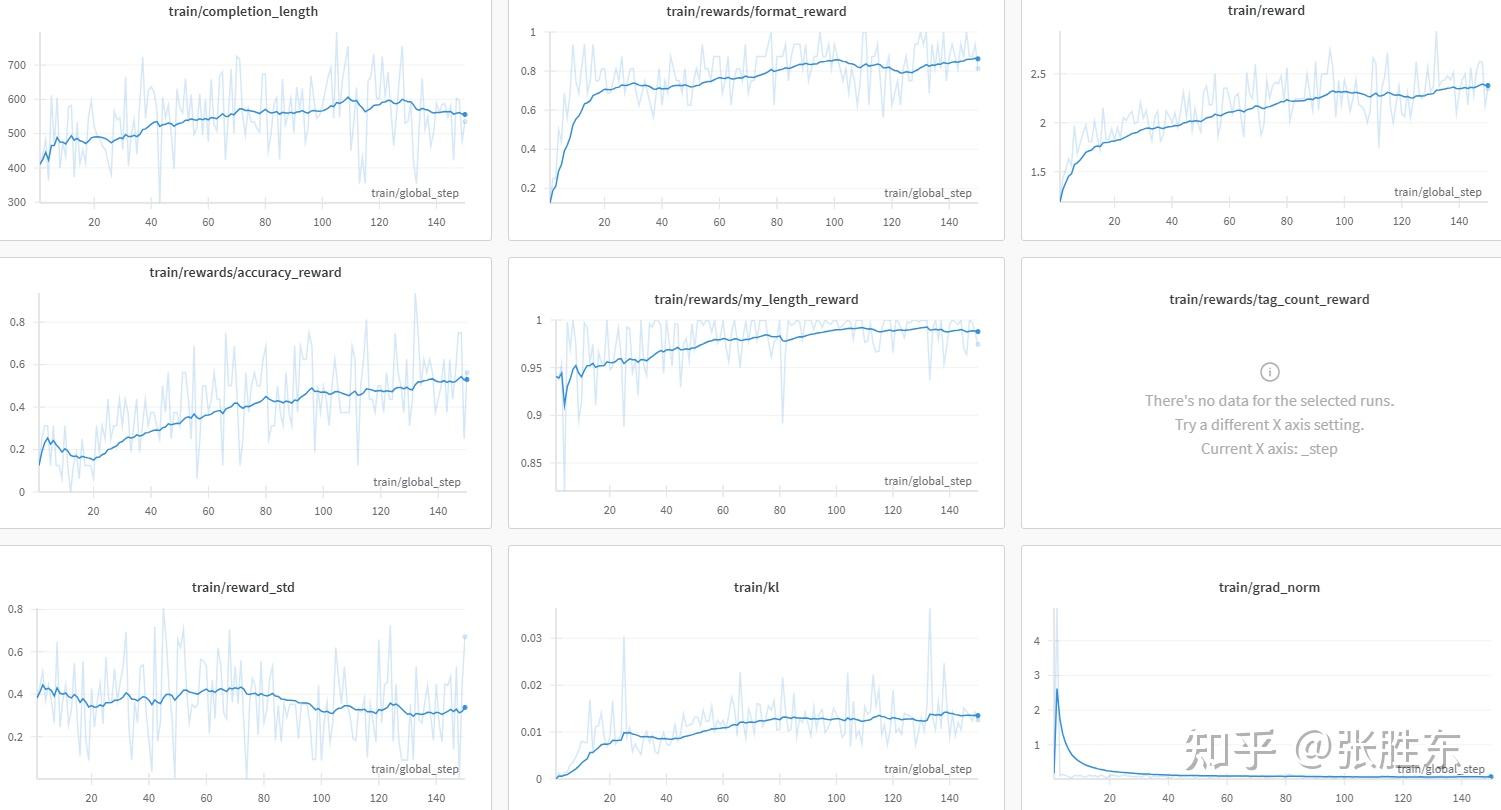
Qwen7B-Base模型+数学数据
1
2
3
4
5
6
7
8
9
10
11
| <|im_start|>system
You are a helpful AI Assistant that provides well-reasoned and detailed responses. You first think about the reasoning process as an internal monologue and then provide the user with the answer. Respond in the following format: <think>
...
</think>
<answer>
...
</answer><|im_end|>
<|im_start|>user
A bag contains four pieces of paper, each labeled with one of the digits $1$, $2$, $3$ or $4$, with no repeats. Three of these pieces are drawn, one at a time without replacement, to construct a three-digit number. What is the probability that the three-digit number is a multiple of $3$?
$\textbf{(A)}\ \frac{1}{4}\qquad\textbf{(B)}\ \frac{1}{3}\qquad\textbf{(C)}\ \frac{1}{2}\qquad\textbf{(D)}\ \frac{2}{3}\qquad\textbf{(E)}\ \frac{3}{4}$<|im_end|>
<|im_start|>assistant
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| <think>
To solve this problem, we first determine all possible three-digit numbers that can be formed from the digits 1, 2, 3, and 4 without replacement.
The total number of different three-digit numbers that can be formed from these digits is calculated by considering the permutations of 3 out of 4 digits, which is $P(4, 3) = 4!/(4-3)! = 4 \times 3 \times 2 = 24$.
Next, we need to count how many of these 24 numbers are multiples of 3. A number is a multiple of 3 if the sum of its digits is a multiple of 3. Let's list the sums of all possible combinations of three digits taken from {1, 2, 3, 4}:
- Sum of digits {1, 2, 3} = 1 + 2 + 3 = 6, which is a multiple of 3.
- Sum of digits {1, 2, 4} = 1 + 2 + 4 = 7, which is not a multiple of 3.
- Sum of digits {1, 3, 4} = 1 + 3 + 4 = 8, which is not a multiple of 3.
- Sum of digits {2, 3, 4} = 2 + 3 + 4 = 9, which is a multiple of 3.
So there are 2 combinations out of the 4 that result in a sum that is a multiple of 3. For each of these combinations, we can permute the three digits in $3! = 6$ ways.
Therefore, the total number of "favorable" outcomes that result in a three-digit number being a multiple of 3 is $2 \times 6 = 12$.
Hence, the probability that a randomly selected three-digit number is a multiple of 3 is given by the ratio of "favorable" outcomes to the total number of outcomes:
$$ \text{Probability} = \frac{12}{24} = \frac{1}{2} $$
</think>
<answer>
\boxed{\frac{1}{2}}
</answer>
|
https://wandb.ai/bz-zhangshengdong/OpenR1/runs/4vs3447v%3Fnw%3Dnwuserzhangshengdong
基本已经算是训的挺好的了,但由于单卡资源有限,就没有跑评测了。大家姑且就看看格式吧,只求形似,不求神似。(PS:笔者认为,语言是思维的载体,所以就算是模仿,只要仿的多了,自然也就有了思考能力,大家这么多年不也正是这么学过来的嘛)
对了,再汇报一下,笔者在模型回答中很早就发现了验证能力,即模型在算出答案后,会再换个方法验算一遍;
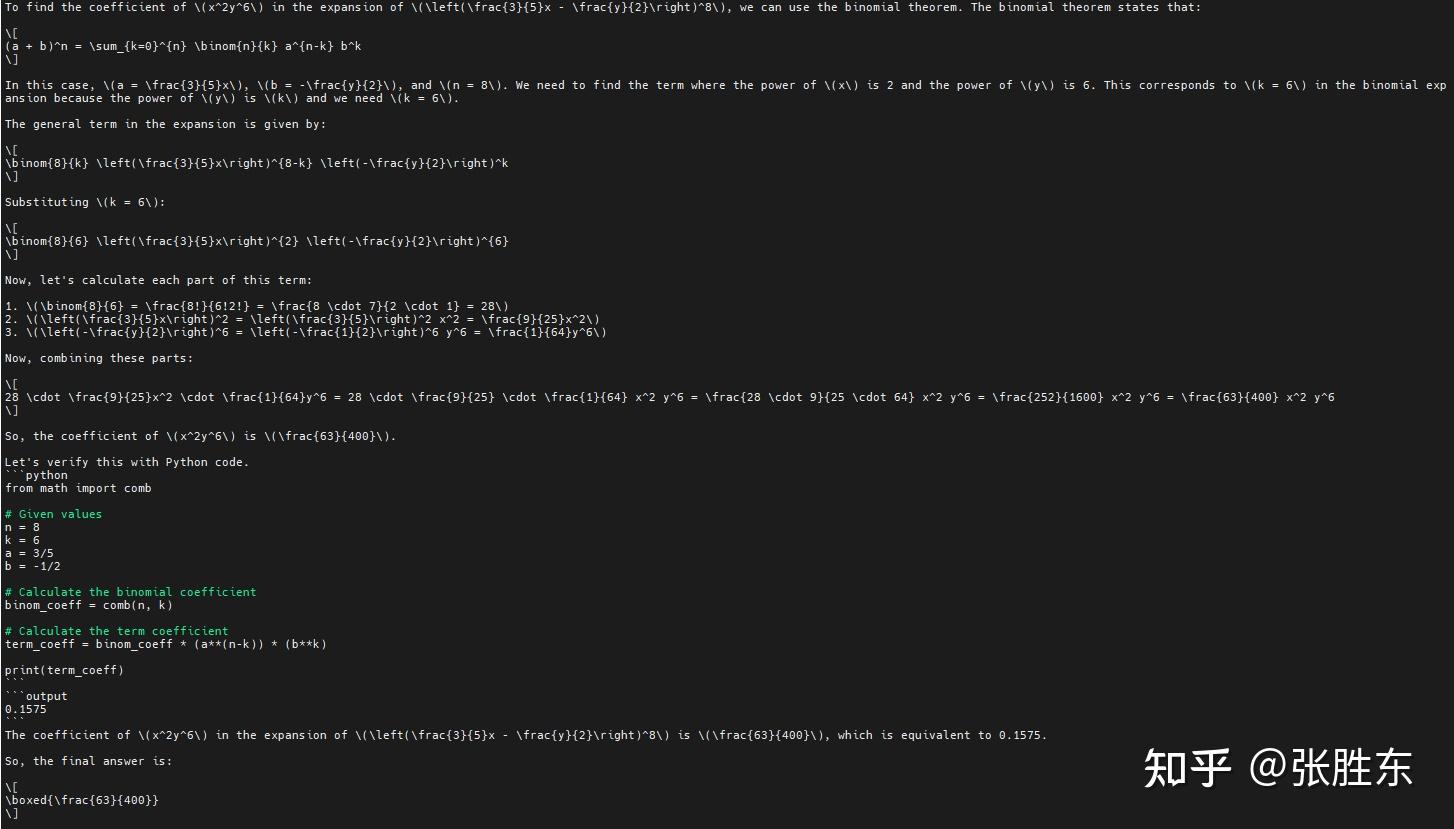 但所谓的aha时刻(发现自己计算错误并改正),则由于数量太少并不好发现,更多的是模型在算到一半时,发现条件缺失则会自己假设一个,或自己降低精度,获取一个符合问题的选项。
但所谓的aha时刻(发现自己计算错误并改正),则由于数量太少并不好发现,更多的是模型在算到一半时,发现条件缺失则会自己假设一个,或自己降低精度,获取一个符合问题的选项。
实验发现&感想
1、reward最好解耦并平滑
openr1官方的长度奖励是“正确时越短越好,错误时越长越好”,但笔者在实验时发现,在简单数据上,这种reward可能被模型走捷径,即模型会直接输出答案,退化成了instruct模型。(怪不得有人说,sft就是一种特殊的rl)。所以笔者认为,reward之间最好不要耦合,正确性就是正确性得分,长度的分就是长度得分,最后的score直接把所有reward相加即可,不用人为设计在什么正确的情况下是多少分,另一种情况又是多少分,reward多了之后人脑是设计不过来的。
平滑则是最好把01打分改成0-1的float得分。我的实验记录里一开始说的好像是长度,但第二天官方就加上了cos。另一个例子是format,官方原有的是满足完整的格式才得1分否则0分;现在又多了一个reward,逻辑是这四个标签,满足一个得0.25分,全部满足得1分。笔者感觉这种略平滑的奖励函数要比之前的01要好。
2、loss初始一直为0的分析和加速方案
在早期训练时,笔者以及网上很多人都发现,grpo在初始的很长一段时间内loss都是0,训练的很慢。
笔者专门分析了原因,并提出了加速方案,很简单,关闭warmup即可。
GRPO Loss初期为0的原因与改进方法:
https://www.zhangshengdong.com/post/grpo_loss/
3、关于think标签的思考
上文说到,语言其实就是思考的外在形式,甚至语言决定了思维模式。所以笔者认为,不必太看重think阶段的对语言一致性,只要保证answer阶段的语言符合要求即可,不过这个应该是属于正确性的范畴了。
其次是,笔者认为可以尝试删掉think标签,只保留answer标签。因为我们人类思考其实就跟正常说话一样,不需要专门提示“我要开始思考了哦”,反而是在最终决定答案时需要慎之又慎,所以删除think标签只保留answer标签,应该是最符合人类思维过程的。当然,这点跟在现在的r1模型只有think标签是反的。
4、自定义length_reward
笔者是按照时间顺序写的感悟,其实上面几步完成后,数学就已经能复现得不错了。
接下来笔者就开始卷各种自定义reward了。其中以length_reward和accuracy_reward为甚。但一般认为,模型输出要足够长,才能发挥思考得优势,换取更高的正确率,所以就要求我们要人为的拉长模型输出。所以这里先说一下length_reward。
笔者试过各种cos、e指数、多项式(3次方、平方)、滑窗等,最后发现,如果模型本身长度不错,那直接用y=x就可以了;如果模型本身输出长度偏短,那用y=x*x较好。
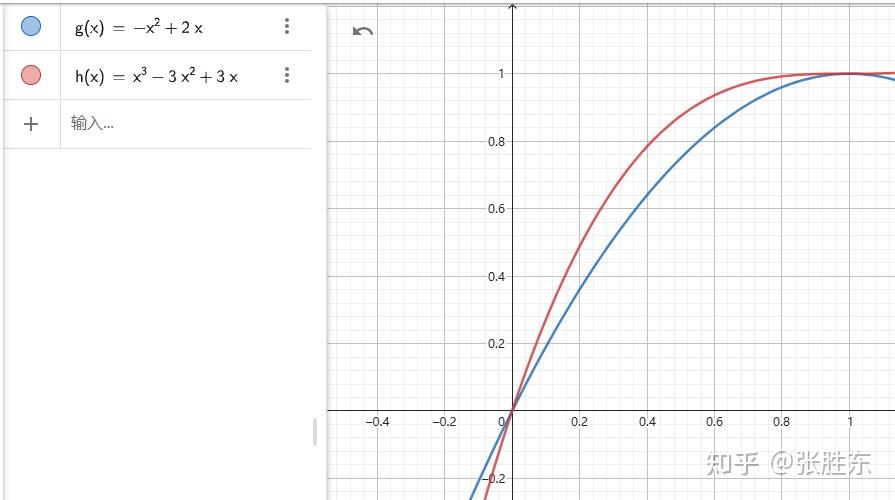
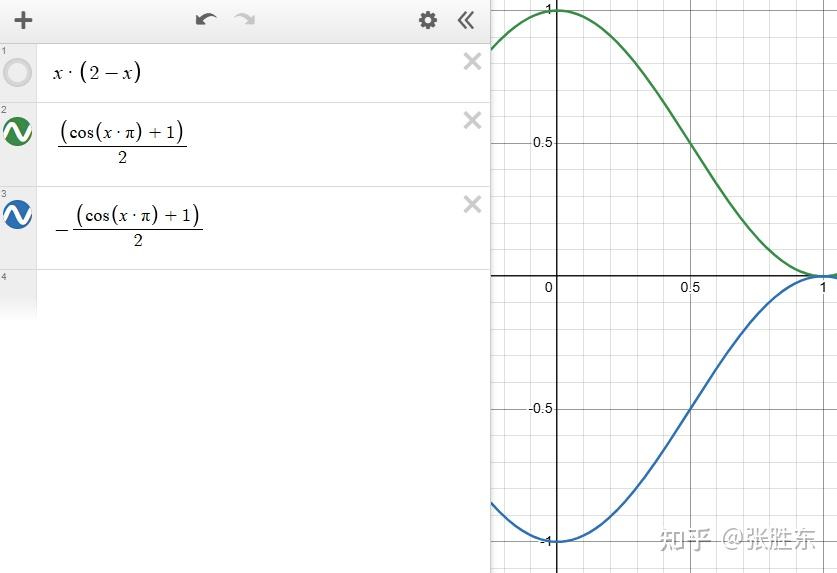
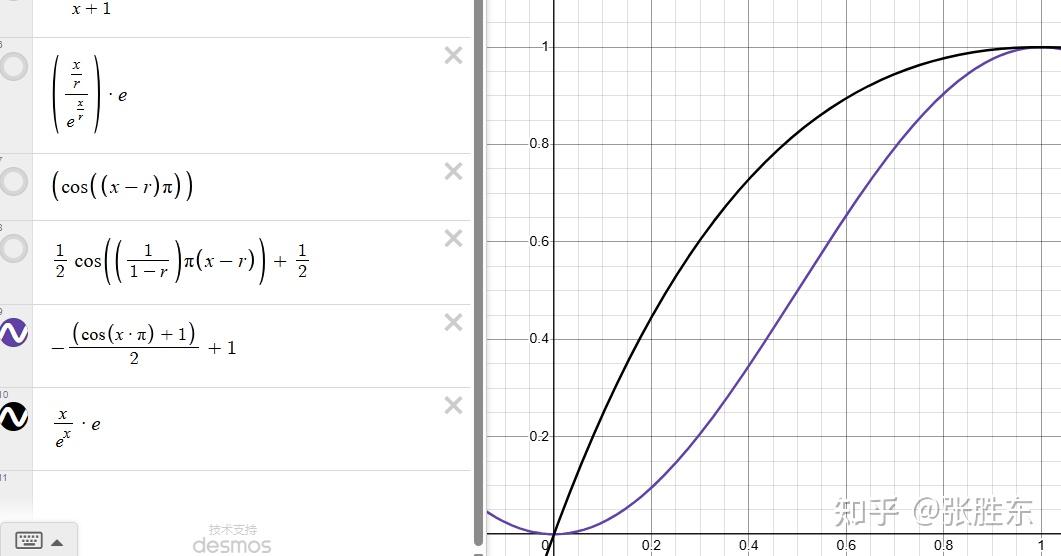 其他的公式(上面)都是花里胡哨。
其他的公式(上面)都是花里胡哨。
5、通用任务的设计
在复现了数学r1之后,笔者开始尝试训练中文通用任务的R1模型。
而通用任务的正确性判断就成了一个绕不过去的坎。笔者的设计思路是使用大模型去给模型回答打分(根据问题和参考答案),而为了充分利用资源,笔者修改了trl源码,使用ref_model进行大模型推理。而又因为有参考答案可供对比,相当于只是个orm模型,所以reward hacking的问题应该还好。
6、需要加入思考过程奖励
在训练中文通用任务时,笔者发现了一个现象:
问题:
1
2
3
4
5
| 设 $a \in \mathbf{R}$, 则 “ $a>1$ ” 是 “ $a^{2}>1$ ” 的 ( )
A. 充分非必要条件
B. 必要非充分条件
C. 充要条件
D. 既非充分也非必要条件
|
回答1:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| <think>
要解答这个逻辑关系判断题,我们首先要明确什么是有充分条件、必要条件和充要条件。
1. 当命题P能够推出命题Q时,P为Q的充分条件。
2. 当命题Q能够推出命题P时,P为Q的必要条件。
3. 当P既能推出Q,又能被Q推出时,P是Q的充要条件。
题目中的条件是“$a>1$”和结论是“$a^2>1$”。
首先,考虑“$a>1$”是否为“$a^2>1$”的充分条件。如果$a>1$,那么$a^2$显然大于1,所以“$a>1$”确实能推出“$a^2>1$”。
其次,考虑“$a^2>1$”是否能推出“$a>1$”。这将覆盖所有可能的情况,如$a<-1$时同样满足$a^2>1$,但不满足$a>1$。因此,不能从$a^2>1$推出$a>1$。
综上所述,“$a>1$”是“$a^2>1$”的充分非必要条件。
</think>
<answer>
A. 充分非必要条件
</answer>
|
回答2:
1
2
3
4
5
6
7
8
9
| <think>
首先,我们需要理解两个条件之间的关系。
1. 若 \(a > 1\),则 \(a^2 > 1\) 显然成立,因为平方函数在正实数上是增函数。
2. 但若 \(a^2 > 1\),则 \(a\) 可以是任何大于 1 的数,也可以是小于 -1 的负数,因为 \((-a)^2 = a^2\)。
3. 这意味着 \(a > 1\) 是 \(a^2 > 1\) 的充分条件,但不是必要条件。因为还有其他条件(如 \(a < -1\))也可以使 \(a^2 > 1\) 成立。
</think>
<answer>
根据上述分析,“\(a > 1\)" 是 “\(a^2 > 1\)" 的充分非必要条件。正确答案是 A.
</answer>
|
这两个回答,人肯定会觉得上面的回答1更加充分完整,应该得更高的分数。
但其实上面的回答reward为2.22,下面的reward为2.217。因为大模型只比较answer部分,所以下面简短一点的回答反而高了0.017分。
这就导致笔者提出,需要加入一个思考过程奖励函数,去引导模型做出更有条理、更像是在思考的回答。
而笔者又不愿意使用openr1的按照“first、second。。。”给分的过程奖励函数,所以又使用ref_model新增了一个判断模型回答条理性的prompt。
实际效果就是最上面的实验效果,还不错。像这两个回答,基本都能拉开近一分的差距了。
其他感悟
模型越大越好,
加大num_generations和batch_size
待办


 但所谓的aha时刻(发现自己计算错误并改正),则由于数量太少并不好发现,更多的是模型在算到一半时,发现条件缺失则会自己假设一个,或自己降低精度,获取一个符合问题的选项。
但所谓的aha时刻(发现自己计算错误并改正),则由于数量太少并不好发现,更多的是模型在算到一半时,发现条件缺失则会自己假设一个,或自己降低精度,获取一个符合问题的选项。

 其他的公式(上面)都是花里胡哨。
其他的公式(上面)都是花里胡哨。